Transformer的Attention及其各种变体：全面详解MHA、MQA、GQA和MLA

Feb 25, 2025 · 冷眸

1. MHA (Multi-Head Attention)
2. KV Cache的产生
3. MQA (Multi-Query Attention)
4. GQA(Group-Query Attention)
5. MLA(Multi-head Latent Attention)

最近大火的 DeepSeek-V3 主要使用了 Multi-head Latent Attention (MLA) 和 DeepSeekMoE。其中 MLA 在 DeepSeek-V2 中已经提出并使用。学习和整理记录一下 Attention 的发展链路，从 MHA -> MQA -> GQA -> MLA。借鉴苏神的解读，缓存与效果的极限拉扯：从 MHA、MQA、GQA 到 MLA，写写自己的学习记录。

mla1

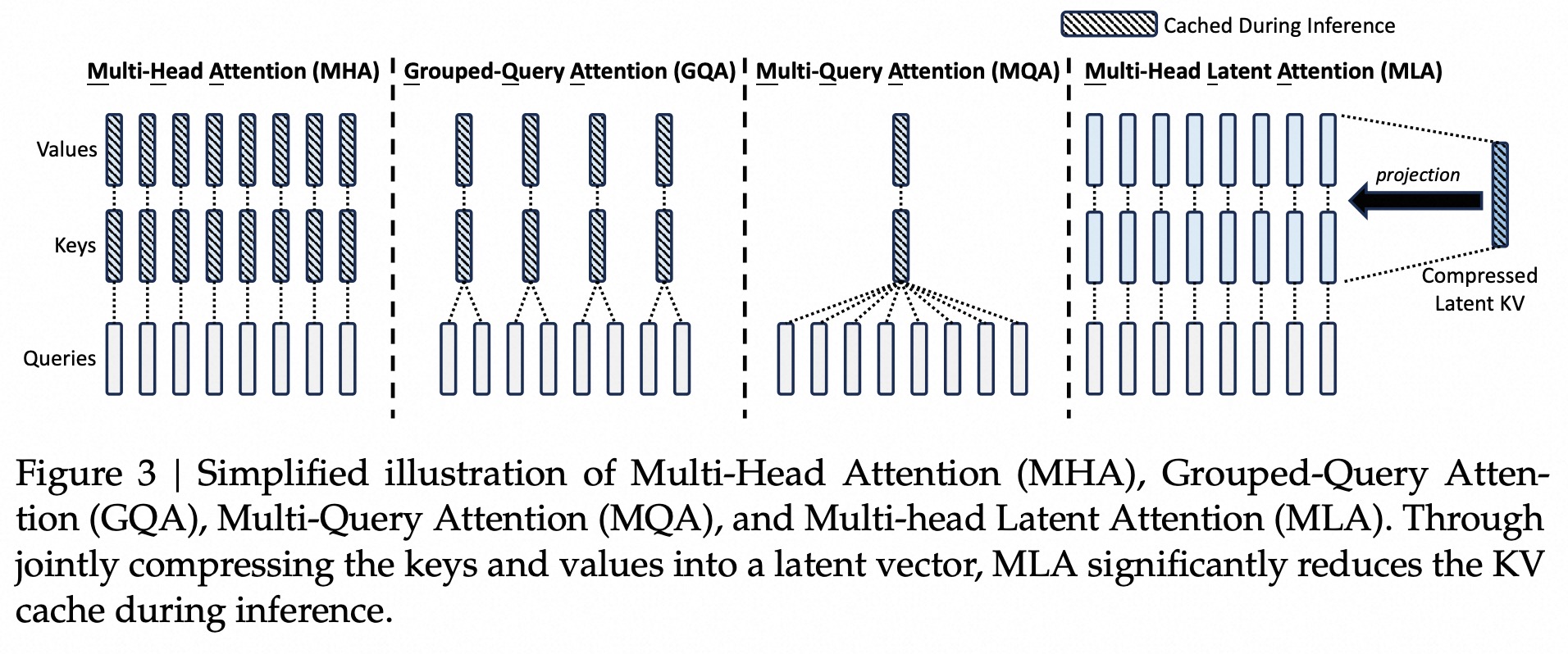
1. MHA (Multi-Head Attention)

Multi-Head Attention，源自 2017 年论文《Attention is All You Need》，将 QKV 在 dim 维度上进行分割为多个独立的 head，每个 head 单独计算 attention，再将结果进行拼接。

假设输入序列为 $ x_1, x_2, \dots, x_t $，其中 $ x_i $ 的维度为 $ d $。我们知道分割和复制其实都是简单的线性映射关系，可以用矩阵进行表示，因此我们在下面可以使用一个线性矩阵 $ W_q^{(s)} $ 来表示输入向量 $ x_i $ 到第 $ s $ 个 head 上特征的映射（其实里面包含两部分：先将向量映射为 query，再将 query 分割为多个 head 的 $\text{query}_h$）。

第 $ s $ 个 head 上的 attention 变换如下，第 $ t $ 个 query 和 1-t 的 key 和 value 计算 attention，将多个 head 的结果进行拼接输出，得到时刻的 MHA 输出，其中$ d_k = d_v = d / h $：

$$ q_i^{(s)} = x_i W_q^{(s)} \in \mathbb{R}^{d_k}, \quad k_i^{(s)} = x_i W_k^{(s)} \in \mathbb{R}^{d_k}, \quad v_i^{(s)} = x_i W_v^{(s)} \in \mathbb{R}^{d_v} $$

$$ o_t^{(s)} = \text{Attention} \left( q_t^{(s)}, k_{\leq t}^{(s)}, v_{\leq t}^{(s)} \right) \triangleq \frac{\sum_{i \leq t} \exp(q_t^{(s)} k_i^{(s)T}) v_i^{(s)}} {\sum_{i \leq t} \exp(q_t^{(s)} k_i^{(s)T})} $$

$$ o_t = \text{Concat} \left( o_t^{(1)}, o_t^{(2)}, \dots, o_t^{(h)} \right) $$

优点：

多头并行计算，提升效率；
每个head可以关注不同子空间的特征信息，丰富表达能力。

缺点：

每次生成都需要计算历史的QKV矩阵，显存和计算量较大。

2. KV Cache的产生

为了缓解上述缺陷，引入KV Cache，将历史每个head的key和value缓存起来，避免不必要的重复计算，减少计算量，本质是通过空间换时间的方式提升推理速度。

KV Cache存在的问题： KV Cache在缓存KV时占用显存，且KV Cache的大小与序列长度是线性相关的。如果输入序列长度越来越大，可能会导致模型KV Cache大小超过单卡的显存量，基于"卡内通信带宽 > 卡间通信带宽 > 机间通信带宽" 原理，使得模型在长文本推理时速度变慢。

缓解上述问题方案： 在尽可能保证效果的前提下(减少KV意味着减少特征信息)，减少KV Cache的大小，使得模型在更少的设备上推理更长的文本。

因此MQA和GQA和MLA都是为了在尽可能保证效果的同事，减少KV Cache的大小，对MHA进行改进。

3. MQA (Multi-Query Attention)

Multi-Query Attention，源自 2019 年的论文 《Fast Transformer Decoding: One Write-Head is All You Need》，是每个 head 计算 attention 时，每个 head 的 K、V 都共享，只有 Q 在不同 head 是不同的。这样 KV Cache 只用缓存一个 head 的 K 和 V，降低为 MHA 的 KV Cache 大小的 1/h。

$$ q_i^{(s)} = x_i W_q^{(s)} \in \mathbb{R}^{d_k}, \quad k_i = x_i W_k \in \mathbb{R}^{d_k}, \quad v_i = x_i W_v \in \mathbb{R}^{d_v} $$

$$ W_q^{(s)} \in \mathbb{R}^{d \times d_k}, \quad W_k \in \mathbb{R}^{d \times d_k}, \quad W_v \in \mathbb{R}^{d \times d_v} $$

$$ o_t^{(s)} = \text{Attention} \left( q_t^{(s)}, k_{\leq t}, v_{\leq t} \right) \triangleq \frac{\sum_{i \leq t} \exp(q_t^{(s)} k_i^{T}) v_i} {\sum_{i \leq t} \exp(q_t^{(s)} k_i^{T})} $$

$$ o_t = \text{Concat} \left( o_t^{(1)}, o_t^{(2)}, \dots, o_t^{(h)} \right) $$

可以看到，$ k_i, v_i $ 没有上标 $ s $ 了，KV 没有了 head 的概念。

优点：

节省显存，KV Cache降低为原始的1/h;
减少计算和通信开销，提升推理速度。

缺点：

性能下降：KV Cache压缩过于严重，影响模型训练稳定性和模型效果。

4. GQA(Group-Query Attention)

Group-Query Attention，源自2023年论文《GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints》。为了解决MQA KV Cache过度压缩的问题，提出了MQA和MHA中间版本，将所有Head分为g组(g可以是整数，便于repeat到h个head)，每个组共享各自的K、V。

其做法：将每一份K和V均分为$g$组$d=g*d_{head}$，然后每组的KV repeat $h/g$次，正确实现每个head所需要的KV。

$$ q_i^{(s)} = x_i W_q^{(s)} \in \mathbb{R}^{d_k}, \quad k_i^{([sg/h])} = x_i W_k^{([sg/h])} \in \mathbb{R}^{d_k}, \quad v_i^{([sg/h])} = x_i W_v^{([sg/h])} \in \mathbb{R}^{d_v}, $$ $$ o_t^{(s)} = \text{Attention} \left( q_t^{(s)}, k_{[sg/h]}^{\leq t}, v_{[sg/h]}^{\leq t} \right) \triangleq \sum_{i \leq t} \frac{\exp(q_t^{(s)} (k_i^{[sg/h]})^\top)}{\sum_{i \leq t} \exp(q_t^{(s)} (k_i^{[sg/h]})^\top)} v_i^{[sg/h]} $$ $$ o_t = \text{Concat} \left( o_t^{(1)}, o_t^{(2)}, \dots, o_t^{(h)} \right) $$

当$g=h$时就是MHA，当g=1时就是MQA。在llama2/3-70中，其他使用GQA同体量的模型也设置$g=8$，正好每张卡片可以负责计算一组K和V的Attention，保证KV多样性的同时减少时间通话。

优点：

性能和效率之间平衡：保证KV多样性同时，减少KV Cache大小；
稳定性：相比MQA，训练过程较为稳定；

缺点：

需人为合理设置组数g。

5. MLA(Multi-head Latent Attention)

mla2

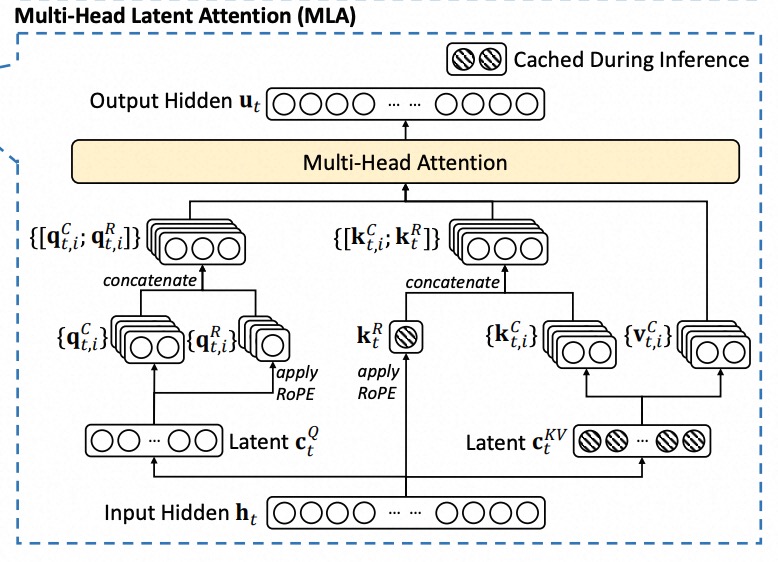
Multi-head Latent Attention通过降维的方式缓解KV Cache显存占用过大问题，只看上面的图还是比较难理解的，接下来看看怎么做的。带着两个问题去看，MLA如何通过Latent Vectore实现减小KV Cache的大小？MLA如何和RoPE进行结合？

5.1 MLA without RoPE

为了方便理解，我们先看看不使用RoPE的MLA实现。

实现方式：

通过一个低秩矩阵将输入 $x_i \in \mathbb{R}^d$ 降维映射为 $c_i \in \mathbb{R}^{dc}$（论文中叫latent vector，它没有上标(S)说明与head无关，多head之间是共享的），于是原始KV Cache缓存每个head的 $k_i^{(s)}, v_i^{(s)}$ 变为缓存在；然后在通过扩维矩阵 $W_k^{(s)}$ 和 $W_v^{(s)}$ 将 $c_i \in \mathbb{R}^{dc}$ 映射为 $k_i^{(s)}, v_i^{(s)}$，后续就执行Attention就行了。

低秩映射：$c_i = x_i W_c \in \mathbb{R}^{dc}, \quad W_c \in \mathbb{R}^{d \times dc}$

$$ q_i^{(s)} = x_i W_q^{(s)} \in \mathbb{R}^{dk}, \quad k_i = c_i W_k^{(s)} \in \mathbb{R}^{dk}, \quad v_i = c_i W_v^{(s)} \in \mathbb{R}^{dv} $$

$$ o_t^{(s)} = \text{Attention} \left( q_t^{(s)}, k_{[s]}^{\leq t}, v_{[s]}^{\leq t} \right) \triangleq \sum_{i \leq t} \frac{\exp(q_t^{(s)} (k_i^{(s)})^\top)}{\sum_{i \leq t} \exp(q_t^{(s)} (k_i^{(s)})^\top)} v_i^{(s)} $$

$$ o_t = \text{Concat} \left( o_t^{(1)}, o_t^{(2)}, \dots, o_t^{(h)} \right) $$

存储大小变化：

存储大小由 $2 * n_h * d_h * l \Rightarrow d_c * l$，其中$n_h$表示head的数量，$d_h$表示每个head的 $k_i^{(s)}, v_i^{(s)}$ 的dim，$l$表示layers的数量，$d_c \ll (n_h d_h)$表示的$c_i$的维度。

矩阵吸收合并：

这样虽然减少了存储，但推理时每次都经过升维矩阵运算得到K、V，没有减少计算量？其实过程中，可以使用矩阵吸收(absorbed)的方式将矩阵进行合并。

$$ q_t^{(s)} k_i^{(s)T} = \left( x_t W_q^{(s)} \right) \left( c_i W_k^{(s)} \right)^\top = x_t \left( W_q^{(s)} W_k^{(s)T} \right) c_i^T $$

这样在Q和K计算时，权重矩阵 $W_q^{(s)} W_k^{(s)}$ 可以合并在一块；同时 $W_v^{(s)}$ 可以吸收到 $o_t$ 上，被Concat后的网络层权重吸收合并。这样就让 $c_i$ 直接参与计算，不需要再额外计算出来K和V。

Q矩阵降维：

在DeepSeek-V2中，为了节约训练过程中的参数量，也对Q进行了低秩投影，这个与KV Cache无关。将上述Q的计算方式换成下列方式。

$$ c_i’ = x_i W_c \in \mathbb{R}^{dc}, \quad q_i^{(s)} = c_i’ W_q^{(s)} \in \mathbb{R}^{dk}, \quad W_c \in \mathbb{R}^{d \times dc}, \quad W_q^{(s)} \in \mathbb{R}^{dc \times dk} $$

5.2 MLA推理过程

通过矩阵吸收合并，以上可以简化为：

$$ c_i’ = x_i W_c’ \in \mathbb{R}^{dc}, \quad c_i = x_i W_c \in \mathbb{R}^{dc} $$ $$ q_i^{(s)} = \left[ c_i’ W_q^{(s)} W_k^{(s)T}, c_i’ W_q^{(s)} R_i \right] \in \mathbb{R}^{dc+dr}, \quad W_q^{(s)} \in \mathbb{R}^{dc \times dk}, \quad W_k^{(s)} \in \mathbb{R}^{dk \times dc}, \quad W_q^{(s)} \in \mathbb{R}^{dc \times dr} $$ $$ k_i^{(s)} = [c_i, x_i W_k^{(s)} R_i] \in \mathbb{R}^{dc+dr}, \quad W_k^{(s)} \in \mathbb{R}^{dc \times dr} $$ $$ o_t^{(s)} = \text{Attention} \left( q_t^{(s)}, k_{[s]}^{\leq t}, c^{\leq t} \right) \triangleq \sum_{i \leq t} \frac{\exp(q_t^{(s)} (k_i^{(s)})^\top)}{\sum_{i \leq t} \exp(q_t^{(s)} (k_i^{(s)})^\top)} c_i $$ $$ o_t = \left[ o_t^{(1)} W_v^{(1)}, o_t^{(2)} W_v^{(2)}, \dots, o_t^{(h)} W_v^{(h)} \right] $$

此时，KV Cache只缓存 $c_i, x_i W_k R_i$ 这两项就可以。 存储大小变化为 $(dc + dr)l$，注意可以发现V没有了，V被分为两部分了，$c_i$ 被放在Attention中的分子部分，$W_v^{(s)}$ 被吸收到 $o_t$ 上。

总结：MLA即达到了降低KV Cache大小的作用，还实现添加了RoPE，虽然带了点计算量（降维和升维）。

5.3 DeepSeek中MLA表达

上面苏神的公式表达和论文中的公式符号只是存在一点点区别，下面我们看看论文中的表达方法。

Latent Vector计算：

$$ c_t^Q = W^{DQ} h_t, \quad c_t^{KV} = W^{DKV} h_t $$

Query计算：

$$ \left[ q_t^{C,1}; q_t^{C,2}; \dots; q_t^{C,nh} \right] = c_t^C = W^{UQ} c_t $$ $$ \left[ q_t^{R,1}; q_t^{R,2}; \dots; q_t^{R,nh} \right] = q_t^R = \text{RoPE}(W^{QR} c_t^C) $$ $$ q_t,i = [q_t^{C,i}, q_t^{R,i}] $$

Keys计算：

$$ \left[ k_t^{C,1}; k_t^{C,2}; \dots; k_t^{C,nh} \right] = k_t^C = W^{UKV} c_t^{KV} $$ $$ k_t^R = \text{RoPE}(W^{KR} h_t) $$ $$ k_t,i = [k_t^{C,i}, k_t^{R,i}] $$

Values计算：

$$ v_t^{C,1}; v_t^{C,2}; \dots; v_t^{C,nh} = v_t^C = W^{UV} c_t^{KV} $$

Attention及输出：

$$ o_{t,i} = \sum_{j=1}^{t} \text{softmax} \left( \frac{q_{t,i}^{\top} k_{j,i}}{\sqrt{d_h + d_h^R}} \right) v_{j,i}^{C} $$

$$ u_t = W^O \left[ o_{t,1}; o_{t,2}; \dots; o_{t,nh} \right] $$

顺序与4.2章节"解释QK加入RoPE"部分的表达式对应，只是公式符号发生了点变化。

其中输入序列变化为 $h_t \in \mathbb{R}^d$;
$W^{DQ}, W^{DKV}$分别为Q和KV的低秩投影矩阵（降维）；
$W^{UQ} \in \mathbb{R}^{dk \times nh * d_c}$（多Head）负责query进行升维，
$W^{UK} \in \mathbb{R}^{dh \times nh * d_c}$（多头）负责生成keys和values中不带RoPE部分，
$W^{QR} \in \mathbb{R}^{dh * nh \times d_c}$（多头）和$W^{KR} \in \mathbb{R}^{dh \times nh \times d_r}$（多头）负责keys和values中带有RoPE的部分。

推理过程中，只需要缓存 $c_t^{KV} \in \mathbb{R}^{dc + d_R}$ 以及 $k_t^{R}$ 即可，存储大小为 $(dc + d_R)l$。同时可以将 $W^{UK}$ 吸收到 $u_t$ 上，$W^{UV}$ 吸收到 $W^O$，对于每个query不需要再计算keys和values了。

优势：

长文本推理：kV Cache减小，可以对超长文本进行推理；
性能优势：通过低秩投影和矩阵吸收的方式，性能比MHA更好。